We formulate an equation describing a general Non-Line-of-sight (NLOS) imaging measurement and analyze the properties of the measurement in the Fourier domain regarding the spatial frequencies of the scene it encodes. We conclude that for a relay wall with finite size, certain scene configurations and features are not detectable in an NLOS measurement. We then provide experimental examples of invisible scene features and their reconstructions, as well as a set of example scenes that lead to an ill-posed NLOS imaging problem.

Limited NLOS Measurements Scenario. a,b. refers to two types of forward (confocal & non-confocal) models. These types of integration are known as spherical or elliptical (ellpsoidal) Radon integral. We focus on illustrating how much information is encoded by the limited aperture.

Local Fourier Cone Description. Left and Right show the illustration of the local Fourier cone description for the NLOS measurement from a limited aperture. There are three cones shown in the graph, the planar approximation results from the classical projection slice theorem, confocal measurement refers to the confocal NLOS measurement, complete measurement refers to the single point non-confocal measurement. As we see, the planar approximation cone gives a upper bound on the angle coverage of this Fourier cone. As we can see, this Fourier cone is a spatially varying function. Left. shows this cone changes in vertical direction (depth). Right. shows the Fourier cone move in horizontal direction.

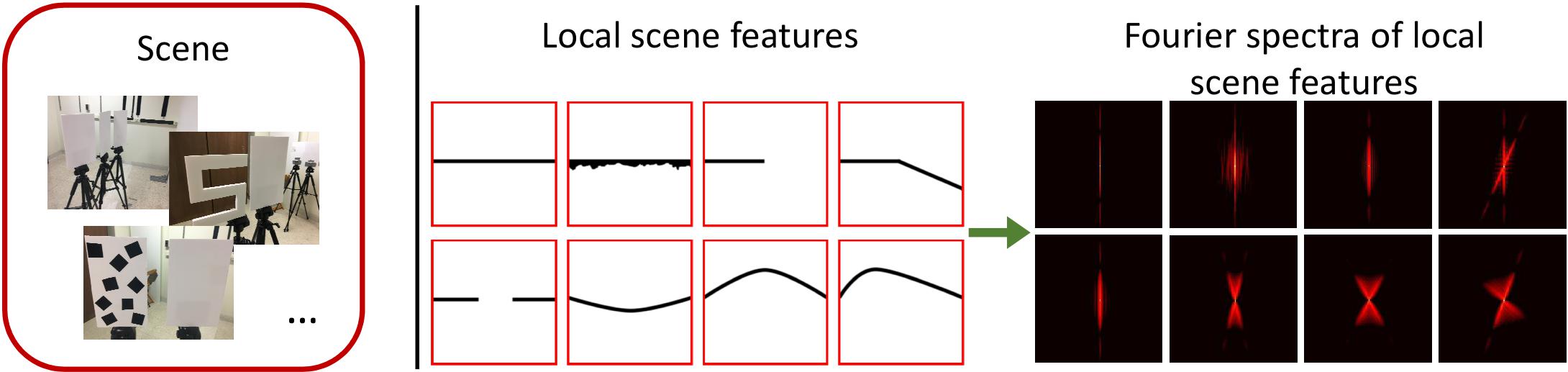
Local scene features. This figure shows a set of common NLOS scene features in the red boxes and their corresponding Fourier transforms. Rotation of the features simply corresponds to rotating by the same angle in the Fourier domain. The patterns are (top left to bottom right) a smooth planar surface, a rough planar surface, the edge of a planar surface, a corner between two surfaces, a gap in a planar surface, a convex curved surface, and two concave curved surfaces. The spectrum of a planar surface is a line. Roughness, curvature, and edges result in spectra that also cover other regions of the Fourier space.

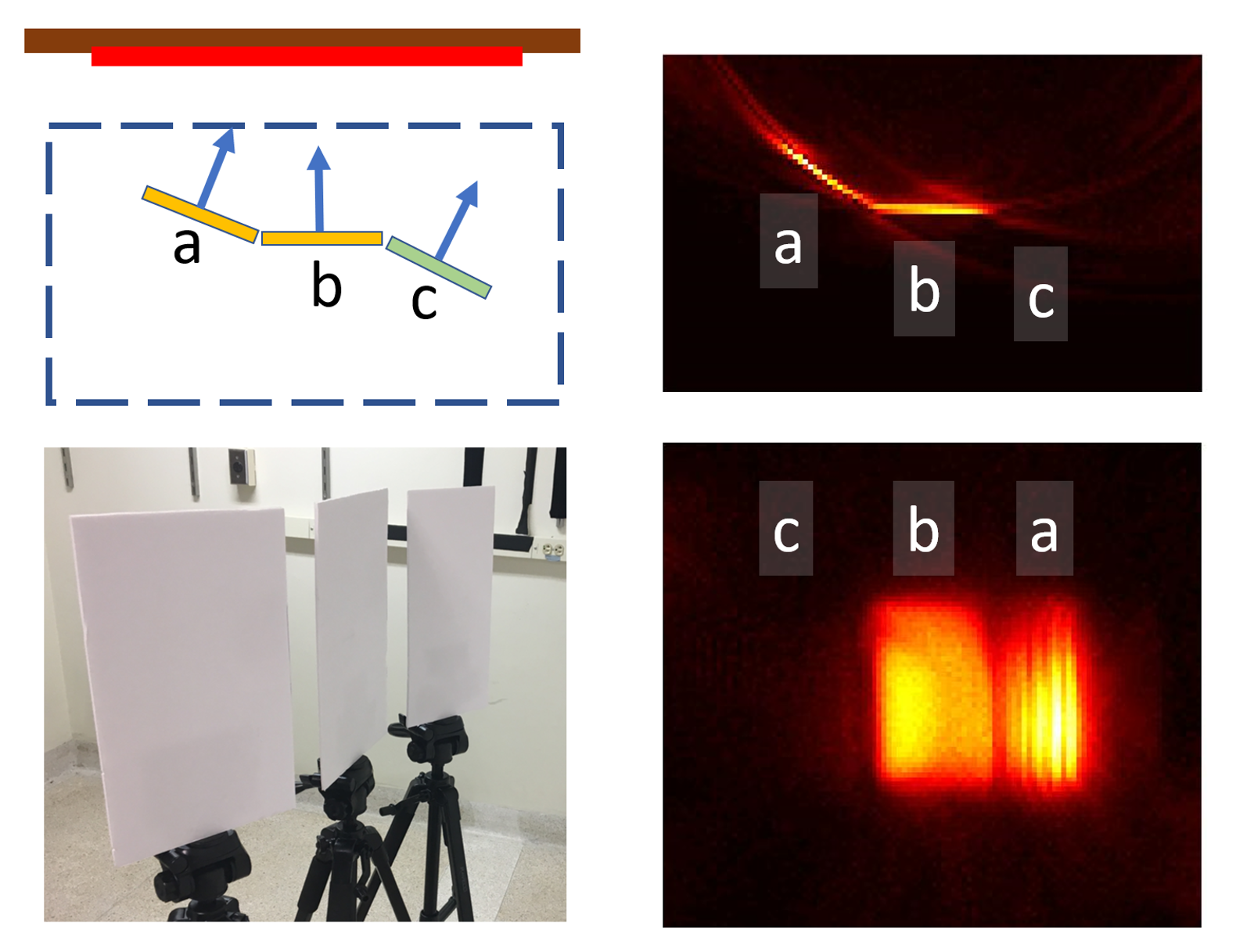
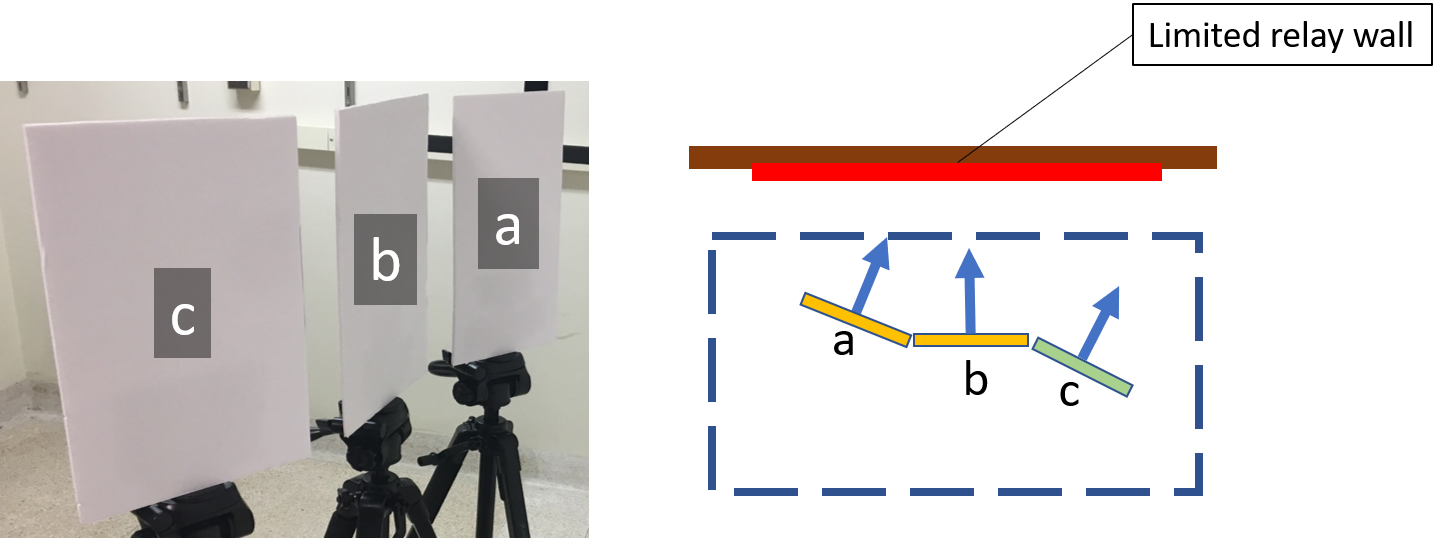
Step1: Let's consider three simple patch examples Patch a & c are in parallel in angle, patch b directly facing the limited relay wall

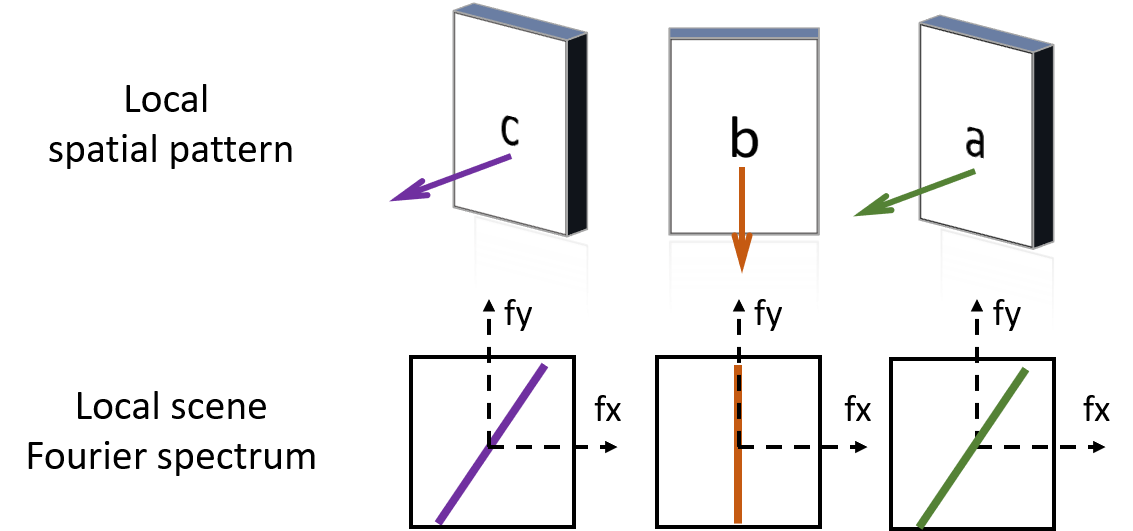
Step2: Local Scene Features and its Fourier Spectrum This illustrates the local cones and the spectra of the plane surfaces.

Step3: Local Fourier Cone and Sampling Features lying inside the cone can be captured by the measurements from the limited aperture.

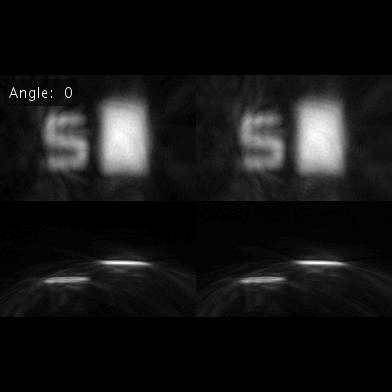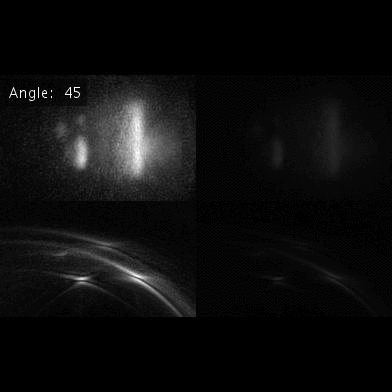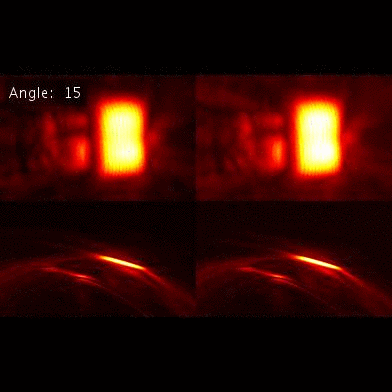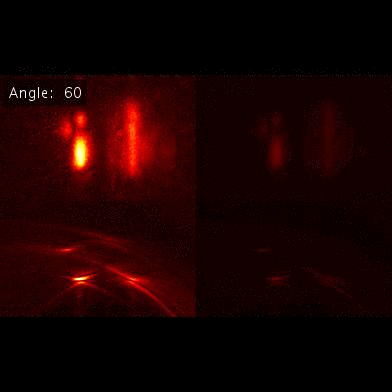
Step4: Missing features lying outside the local Fourier cone Local scene features lying outside the local Fourier cone may not be well-represented by the limited aperture scenario. Considering the fixed limited size sampling wall, even the same target appears completely different when rotated by a tiny angle.

Additional result. Letter S and patch rotation result. This analysis can be further extented to complex surface structures.

This work was funded by DARPA through the DARPA REVEAL project (HR0011-16-C0025), the NASA NIAC program, and the AFOSR through the Young Investigator Program (FA9550-15-1-0208), and the DURIP program (FA9550-18-1-0409).